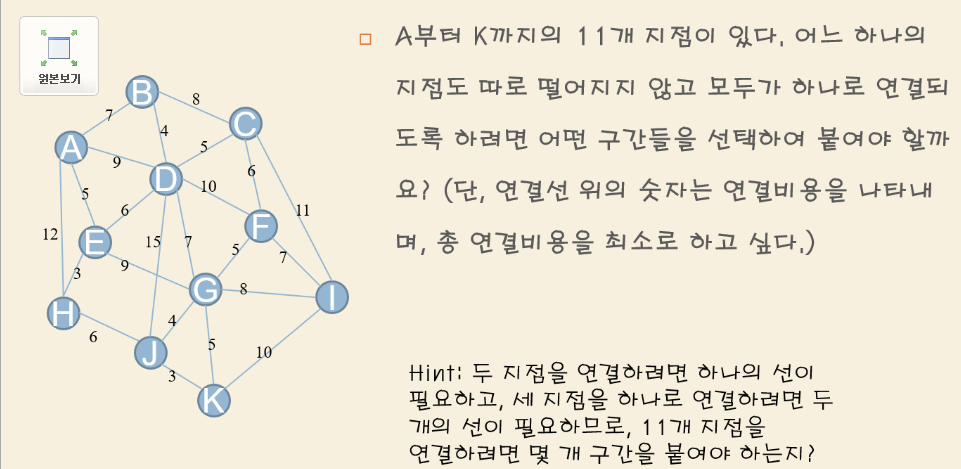
올해초 대학원에 진학했을때, 오리엔테이션주에 어떤 교수님이 이런 문제를 주더라구요.
(참고로 전 경영대학원 다니고 있습니다.)
처음엔 아래사진처럼 노가다로 그냥 다 계산을 했었습니다. ㅋㅋㅋ
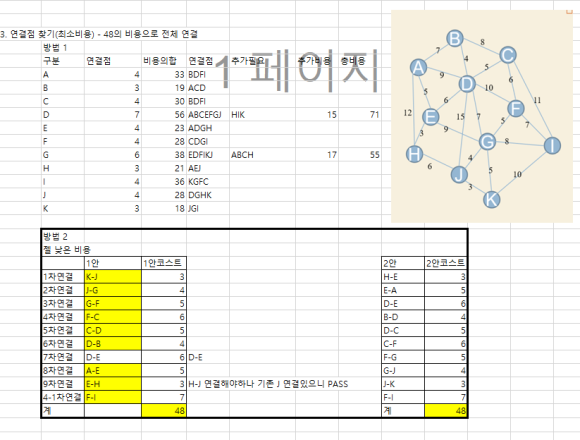
먼저 제일 짧은 구간을 고릅니다.
3인비용이 드는 구간 EH, JK, 이곳 어느곳부터 시작해도 좋습니다.
일단 EH를 칠하고, EH와 연결이 되어있지 않은것중에 작은 라인은 JK 입니다.
그리고 나서 작은 비용인 4를 보면
BD, GJ 가 보입니다. 이것도 실제 그림을 그리면서 연결시켜봅니다.
이런식으로 가다보면, 노가다로 만들수 있습니다.
(자세한 예는 위키백과 첨부합니다)
그런데 이렇게 하나하나 하다보니 시간도 아깝고해서...
알고리즘이 없을까 고민하다가
구글링도 하게되고, 코딩하면 되겠다 싶었습니다.
그렇게 공부하다가 파이썬으로 구현했습니다.
(구글짱...)
#파이썬활용 최소비용 구하기
parent = dict()
rank = dict()
#vertice 초기화
def make_set(vertice):
parent[vertice] = vertice
rank[vertice] = 0
#해당 vertice의 최상위 정점을 찾는다
def find(vertice):
if parent[vertice] != vertice:
parent[vertice] = find(parent[vertice])
return parent[vertice]
#두 정점을 연결한다
def union(vertice1, vertice2):
root1 = find(vertice1)
root2 = find(vertice2)
if root1 != root2:
if rank[root1] > rank[root2]:
parent[root2] = root1
else:
parent[root1] = root2
if rank[root1] == rank[root2]:
rank[root2] += 1
def kruskal(graph):
minimum_spanning_tree = []
for vertice in graph['vertices']:
make_set(vertice)
#간선 weight 기반 sorting
edges = graph['edges']
edges.sort()
#간선 연결 (사이클 없게)
for edge in edges:
weight, vertice1, vertice2 = edge
if find(vertice1) != find(vertice2):
union(vertice1, vertice2)
minimum_spanning_tree.append(edge)
return minimum_spanning_tree
graph = {
'vertices': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H','I','J','K'],
'edges': [
(7, 'A', 'B'),
(9, 'A', 'D'),
(5, 'A', 'E'),
(12, 'A', 'H'),
(8, 'B', 'C'),
(4, 'B', 'D'),
(5, 'C', 'D'),
(6, 'C', 'F'),
(11, 'C', 'I'),
(6, 'D', 'E'),
(10, 'D', 'F'),
(7, 'D', 'G'),
(15, 'D', 'J'),
(6, 'D', 'E'),
(3, 'E', 'H'),
(9, 'E', 'G'),
(5, 'F', 'G'),
(7, 'F', 'I'),
(4, 'G', 'J'),
(5, 'G', 'K'),
(8, 'G', 'I'),
(4, 'G', 'J'),
(6, 'H', 'J'),
(10, 'I', 'K'),
(3, 'J', 'K'),
]
}
kruskal(graph)
-----------------------------------------------------------------
위의 언어를 친다음 실행하면, 결과값이
[(3, 'E', 'H'), (3, 'J', 'K'), (4, 'B', 'D'), (4, 'G', 'J'), (5, 'A', 'E'), (5, 'C', 'D'), (5, 'F', 'G'), (6, 'C', 'F'), (6, 'D', 'E'), (7, 'F', 'I')] 총 48이 나옵니다.
48이 최소비용이라는 것이지요.
이걸 업무에 적용시킬 수 있는게 없을까 고민은 수없이 했지만,
제 업무에는 딱히 ..ㅎ
비슷한 것으로 고민하시는분은 그대로 복사했다가
저 붉은색만 바꿔서 쓰시면 됩니다!!
다덜 시간날때 파이썬을 공부합시다.
'파이썬' 카테고리의 다른 글
| 엑셀과 파이썬 001 (0) | 2023.07.19 |
|---|---|
| 두더지 잡기 게임 (0) | 2022.09.15 |
| 파이선으로 계산기 만들기 (0) | 2022.09.13 |



댓글